For this final exploration we will be observing the relationship between the Euler line of ∆ABC and the Euler line of the medial triangle ∆DEF of ∆ABC. We will come to see that the similarities between these two lines is so close that it will be hard to distinguish between the two! Let's first quickly review what points lie on the Euler line of any aribitrary triangle. There are three points of concurrency that lie on the Euler line: the orthocenter, the centroid, and the circumcenter. The orthocenter is a the point of concurrency for all three altitudes dropped from each vertice. The centroid is the point of concurrency of all three lines constructed from each vertice to the midpoint of the opposite side. The circumcenter is the point of concurrency of the midpoint bisectors of each side. The Euler line of ∆ABC is constructed below.

So if our exploration extends beyond just the Euler line of ∆ABC and adds on the Euler line of ∆DEF what kind of relationship can we expect to see? We know ∆DEF is the medial triangle of ∆ABC, i.e. the vertices of the medial triangle lie on each median of the original triangle, ∆ABC. Are you thinking what I am thinking? I hope so for we are going to see a strong similaritiy between the circumcenters and centroids of the two triangles, because both the circumcenter and centroid are found using the midpoints of each side segment. Check it out below!

It turns out our Euler lines are so close they lie on top of one another! So why is this happening? First, there are some special relationships between the points on the Euler line of any triangle. First, distance from the centroid to the orthocenter is one half the distance from the circumcenter to the centroid: d(G, H) = 2d(C, G). The centroid is always between the circumcenter and the orthocenter. The centroid is also located 1/3 the distance from the perpendicular side and the opposing vertice. Let's begin with the relationship between the two triangles' centroids. We are able to see that both centroids are located in the same spot, hence the corresponding medians of both triangles are concurrent. The picture below shows us our next observation which is the medial triangle shaded dark brown is 1/4 of the total area of ∆ABC, and looking further we can confirm that all four subtriangles have corresponding side lengths. Hence by Side Side Side similarity theorem, ∆DEF ∼ ∆ABC. Therefore, to conclude the relationship between the two centroids we can see that the medians of ∆DEF correspond to the medians of ∆ABC. For example, the median dropped from vertice F intersects the midpoint of side DE which is the same point of intersection of the median dropped from vertice A to side BC (or the median F). Notice the centroid remains 1/3 of the distance from the perpendicular side and the opposing vertice for both triangles, and the centroid remains between the orthocenter and the circumcenter.

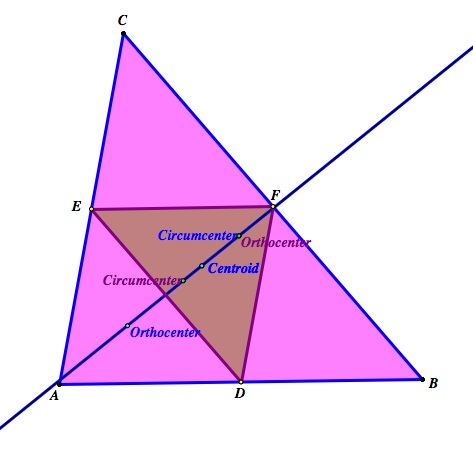
Continuing on with our explorations we move to the relationship between the circumcenters and orthocenters. We can observe from the models above that the circumcenters and orthocenters seem to have swapped locations. This is because our our medians have changed location. Notice the medians dropped from each vertice of ∆ABC intersect large yellow dots which are the medians of ∆DEF. Since the circumcenter is the intersection of a triangles' perpendicular bisectors and the pairs of sides are now parallel our perpendicular bisectors will be parallel, i.e. they will not intersect and therefore will not be located in the same location. To clarify, the perpendicular bisector is EF extends towards the side AB of ∆ABC, we know EF and AB are parallel by the Alternate Interior Angle Theorem where FD or ED is a transversal so the perpendicular bisector of EF will not only be perpendicular to EF, but to AB as well. Conversely, the perpendicular bisector of side AB extend towards EF. Because we already know EF and AB are parallel the perpendicular bisector of AB will also be perpendicular to EF. Since we have two bisectors perpendicular to the same parallel lines we know the two perpendicular bisectors are parallel. Therefore, the circumcenters will not intersect and are on 'opposite sides' of the Euler line.

 

This same reasoning explains why the orthocenters have been switched for orthocenters are also formed by dropping perpendicular lines except this time it is from each vertice. Because the vertices of ∆ABC and ∆DEF are not located in line with one another the orthocenters will be located differently. However, both orthocenters still lie on the Euler line. The circumcenter of ∆ABC and the orthocenter of ∆DEF lie in the same spot. If we look closely and reason through the definitions of a circumcenter and orthocenter we can see that the altitudes of ∆DEF are in fact the perpendicular bisectors of ∆ABC.

 

We have now seen and proven the relationships between the circumcenters, orthocenters, and centroids of triangle ∆ABC and its medial triangle ∆DEF, which then helped us see that the Euler line is the same for both triangles! In fact this relationship continues. Take a look at the medial triangle of the medial triangle below:

The Euler line remains the same and instead of two centroids located in the same spot we now have three centroids located in the exact same spot! The relationship between an arbitrary triangle and its medial traingle is facinating and consistent, and it is important to understand the definitions and properties of the Euler line and medial traingle to further explorations!

 

 

CLICK HERE TO RETURN TO MY FINAL ASSIGNMENT